 Maria's Math Tips, May 2016 |
Welcome to the May edition of my newsletter! 
|
2. Area of rectangles and the Common CoreWhile I feel that most of the Common Core math standards are fairly good, here's one place where I disagree with them.It has to do with the topic when a larger rectangle is broken into TWO parts, and then children write a math sentence from it such as(3 × 4) + (3 × 2). This is in 3rd grade in the CCS. I feel it is a bit too difficult for that level, and would better fit 4th or even 5th grade. Someone just wrote me recently concerning this topic, wondering WHY do we do all this in the first place. Here's my answer.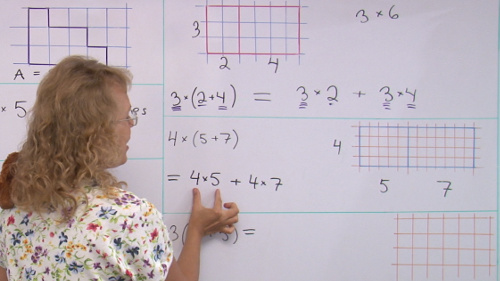 
The reason for breaking the rectangle into two is to get students familiar with this:
7 × (2 + 8) = 7 × 2 + 7 × 8 which is (essentially) the distributive property. The idea is to familiarize the students with how multiplication works with addition, and we use an area model to show or prove that. I decided to edit a video for this topic to help the person who asked: Area of rectangles and the distributive property — video lesson The video just explains HOW we do the rectangle thing, not why. The why is what I just stated above. The distributive property is then studied further in 6th and 7th grades and in algebra. For those grades, you can check out these videos... maybe they will give you a "sneak peek" as to what the 3rd grade stuff is preparing students for:
|
3. First grade math
Check out my collection of free math videos for 1st grade, showing varied exercises for each topic. The videos match Math Mammoth Grade 1 curriculum but will also work no matter which curriculum you follow (in other words, the videos don't rely on you having Math Mammoth curriculum). |
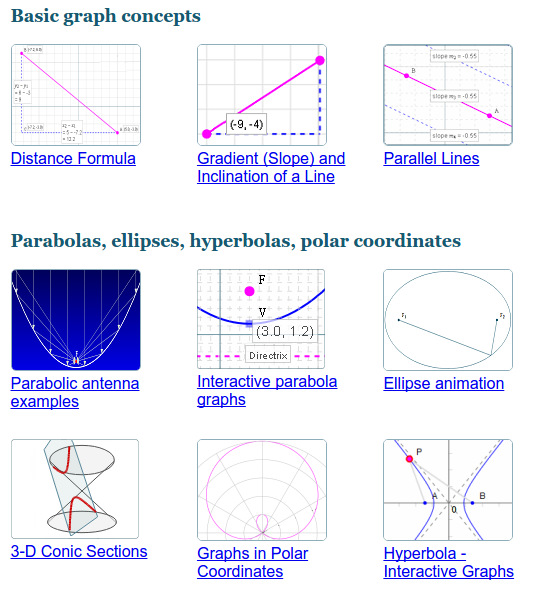
4. Interactivity... for high school mathSome you might be able to use these interactive applications for high school math... they work on various devices plus on an interactive whiteboard. The topics in this collection include graphing, matrices, trigonometry, conic sections, complex numbers, calculus, and vectors. |
5. New cryptographic algorithmsFrom the news...Investigators have created new cryptographic algorithms that are based on particularly hard mathematical problems. They say they would be virtually unbreakable! Cryptographic methods are typically created following the ad-hoc principle: somebody comes up with an algorithm; others attempt to break it — if they don't succeed, it means that the algorithm is secure. The team headed by Prof Dr Eike Kiltz who holds the Chair for Cryptography at the Ruhr-Universität Bochum opted for a different approach. They base their security algorithms on hard mathematical problems. Read more: Hard mathematical problems as basis for new cryptographic techniques Thanks for reading! Feel free to forward this issue to a friend/colleague! Subscribe here. Till next time, Maria Miller |
| Math Mammoth freebies | Math Mammoth on Facebook | Newsletter Archives |
| Inspire4 | Complete curriculum | Placement tests |