Maria's Math News, February 2017

In this newsletter I have a new feature... we are going to LOOK BACK 10 years to the math newsletter I published in February 2007. Seems like a LONG time ago, right? Time just passes SO fast!

In this edition:
  1. Math Mammoth news
  2. Looking back: Ten years ago (grades 1-8)
  3. Dividing into four groups (grades 3-5)
  4. A question on rounding and estimating (grades 4-6)
  5. Find the robber game (grades 2-7)

1. Math Mammoth news

Some of you might be waiting for this announcement...

Math Mammoth Grade 7 South African version is now available!

See free samples and information here.

2. Looking back: Ten years ago

In my newsletter 10 years ago...
  • I included a cute circle terminology song. It just so happens my "middle" child is studying pi right now, so I actually had her listen to this!
  • I featured some magic square addition worksheets that my daughter had greatly enjoyed at that time (Scroll down to item #5 on the page) to practice adding single-digit numbers where the sum goes over 10, such as 7 + 7 and 9 + 5.
  • The site What's Special About This Number? explained (and still explains) what's special about any number up to 9999!
     
  • Ma and Pa Kettle proved themselves good 'mathematicians' in a fun short video! He "proves" by long division that 25 ÷ 5 = 14, and she "proves" by multiplication algorithm that 5 × 14 = 25.

In case you're interested, you CAN still see the old newsletters from February and January 2007. Some links in them are dead though.

3. Dividing into four groups

One Math Mammoth user was stumped by this problem...

There is a picture of 11 apples and it says to "Divide into four groups."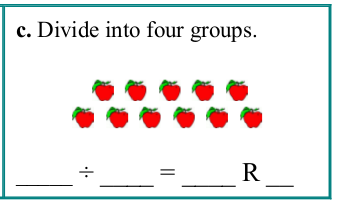



Now, 11 ÷ 4 = 2 R3, clearly. (We get two apples in each group, and three apples left over.) Here comes the part that stumped this lady:
"...if I divide 11 into 4 groups, the groups have to be 2. That leaves a remainder of 3, but then the remainder is bigger than the group. It seems like it could be right anyway, but if you "check" the answer by using 11 ÷ 2, you get 5 R1."

This is an interesting question! There are a few things to keep in mind:
  1. Reminder problems are not checked that way (by using the quotient as the divisor). Instead, you multiply and add.

    For example, to check 23 ÷ 6 = 3 R5, multiply 3 × 6 and then add the remainder 5. You should get the original dividend.
  2. The DIVISOR in division problems can be interpreted to mean two different things: either the number of groups OR the amount in each group.
  3. The rule is: the remainder should not be more than the divisor. It is not that the remainder should not be more than the "group". If you think of the point (2) above, you are either interpreting the division problem as "division into certain size groups", or "division into certain amount of groups". In this case, we have 11 apples to be divided into four groups. The divisor is 4, and it means the number of groups. We get 11 ÷ 4 = 2 R3. The remainder of 3 is NOT more than the divisor (4), so everything is fine! If we had 4 apples left over, we could give each group one more apple, but we have only 3 left over, so we can't.
    4. Then, taking the division 11 ÷ 2 = 5 R1, using the same interpretation, we'd be dividing into TWO groups. That is not going to check the division 11 ÷ 4, where 11 are divided into four groups. The check is always simply to multiply the divisor and the quotient, and add the remainder — and you should get the dividend.

    Hope this helps!

4. A question on rounding and estimating

I got this question from a Math Mammoth user...
In 6A, Rounding and Estimating, the dollar amounts in problem 5 and 6 led me to a question. In question 5 the dollar amount is rounded to the nearest TENTH, but in question 6 it is rounded to the nearest ONE for the apples and TENTH for the cheese. This is our first book we have used and I was wondering if there was a rule we should be following for this procedure? Thank you so much! These books are awesome.

The math problem in question is this:
Elisa bought 7 lb of apples for $1.19 per pound and 3 blocks of cheese for $11.45 a piece. Estimate the total cost.

Here's my answer:

Estimation is not an exact science but depends on your mental math abilities. You round based on what YOU can calculate in your head. And if you can calculate in your head without rounding at all, you're welcome to do even that, but I know most people can't, or wouldn't want to take the time.

So, whether you round to the nearest dollar or nearest ten cents is up to you. Check what kind of number you get -- is it easy to calculate with?

In this case, rounding $11.45 to $11.50 is preferred, because it is still fairly easy to calculate with 1/2 dollar, and it allows less error of estimation than rounding to the nearest dollar (which would make it $11).

The amount $1.19 could have been rounded to $1.20; nothing wrong with that. But then you have 7 x your amount... can you do 7 x $1.20 in your head? If yes, great! (You should be able to!) If not, round to $1.00.

5. Find the robber

In this game, you get to practice coordinates and logical reasoning — where does the robber hide? In how many guesses will you locate him?



After you guess, the game gives you the distance from your guessed point to the robber's location — but according to the city's streets, not as the crow flies.

Fun and fascinating!

=> http://nrich.maths.org/6288



Thanks for reading! :)

Feel free to forward this issue to a friend/colleague! Subscribe here.

Till next time,
Maria Miller
Math Mammoth freebies Math Mammoth on Facebook Newsletter Archives
 
Inspire4 Complete curriculum Placement tests








--